Al principio de la clase de hoy, hemos recordado lo visto el pasado día: "separar" ecuaciones. Cuando tenemos una ecuación cuyo grado es mayor que 2, puesto que no hay fórmulas para las ecuaciones de grado 3, Oliver nos ha enseñado cómo separar una ecuación en partes más pequeñas.
Tenemos dos polinomios que se multiplican entre sí, que son (x-3) . (x-1)= 0
Lo ponemos como ecuación de 2º grado: x2-x-3x+3= 0-----x2-4x+3= 0
a=1; b=2; c=3 } x= 4+-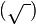
sqrt{\ })">16-12: 2 = 4+-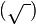sqrt{\ })">4: 2 = 4+2:2=3 y 4-2:2=1
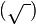sqrt{\ })">16-12: 2 = 4+-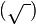sqrt{\ })">4: 2 = 4+2:2=3 y 4-2:2=1Si separamos:
(x-3) . (x-1) = 0
x-3 = 0----Solución: 3
x-1 = 0----Solución: 1} Soluciones 1ª ecuación: 3 y 1
Nota:Si hay varios productos, se separan en varias ecuaciones:
(x-3) . (x+2) . x . (x-1) = 0} Sol: 3; Sol: -2; Sol: 0; Sol: 1
DESCOMPOSICIÓN DE POLINOMIOS:
Si tenemos un polinomio P(x) que se puede escribir como P(x)=Q(x), entonces a es una raíz de P(x).
Ejemplo: P(x)= x3-3x2+2x; pero P(x)=(x2-2x) . (x-1); entonces 1 es una raíz de P(x)
Una raíz de P(x)= (3x7 - 5x4 + 3x2 + 3) . (x - 2)
Por lo que si a es una raíz de P(x), entonces P(x) se puede escribir como P(x)=Q(x) . (x-a)
Ejemplo: P(x)= x3 - 27
¿ Y una raíz?--- 3
Entonces se puede escribir:
P(x) = Q (x) . (x - 3) Que ya veremos cómo calcularlo.
Y esto ha sido la clase del viernes 14 de enero.
Paula Izco Oset 4ºA
saah paulikaaahhhhh!!!!ami no me toka ta dentro d muxo noooo?jaja un besilloooooooo
ResponderEliminar