Martes 25
En la clase de matemáticas vimos :
LOS SISTEMAS DE ECUACIÓN
Tenemos varias ecuaciones que tienen que cumplir las incógnitas y varias incógnitas
Ejemplo:
[3x =4x +7 -5
[4y +3x+7z=4+3x
para que un sistema se pueda resolver "bien" el número de ecuaciones (información que nos dan) tienen que ser igual al número de incógnitas (información que nos piden)

Resolveremos sistemas lineales (de grado 1) de 2 ecuaciones con 2 incógnitas:
a,b,c,A,B,C { ax +by =c
{ Ax +By = C
Son números
1º método (poco útil) para resolver sistemas : GRAFICOS

Consiste en dibujar 2 rectas , cada una dada por cada ecuación

{2x + y = 2 <- La recta son los puntos de coordenada (x,y) que cumplen la igualdad

{x -y =1


Lo que queremos es un valor de "x" y un valor de "y" que cumpla las dos ecuaciones


Donde se corta es la solución

en el punto (1,0) ---> x=1
y=0
Comprobamos { 2.1+0 = 2
{ 1- 0 = 1

Hasta aqui hemos llegado

(lo sienro pero no he podido colocar los graficos..)
Andrea Laquidain 4ºA

Clase de matemáticas del 14/01/11

Viernes 14 de enero del 2011.

Al principio de la clase de hoy, hemos recordado lo visto el pasado día: "separar" ecuaciones. Cuando tenemos una ecuación cuyo grado es mayor que 2, puesto que no hay fórmulas para las ecuaciones de grado 3, Oliver nos ha enseñado cómo separar una ecuación en partes más pequeñas.

Tenemos dos polinomios que se multiplican entre sí, que son (x-3) . (x-1)= 0

Lo ponemos como ecuación de 2º grado: x2-x-3x+3= 0-----x2-4x+3= 0

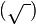a=1; b=2; c=3 } x= 4+-sqrt{\ })">16-12: 2 = 4+-sqrt{\ })">4: 2 = 4+2:2=3 y 4-2:2=1

Si separamos:

(x-3) . (x-1) = 0

x-3 = 0----Solución: 3

x-1 = 0----Solución: 1} Soluciones 1ª ecuación: 3 y 1

Nota:Si hay varios productos, se separan en varias ecuaciones:

(x-3) . (x+2) . x . (x-1) = 0} Sol: 3; Sol: -2; Sol: 0; Sol: 1

DESCOMPOSICIÓN DE POLINOMIOS:

Si tenemos un polinomio P(x) que se puede escribir como P(x)=Q(x), entonces a es una raíz de P(x).

Ejemplo: P(x)= x3-3x2+2x; pero P(x)=(x2-2x) . (x-1); entonces 1 es una raíz de P(x)

Una raíz de P(x)= (3x7 - 5x4 + 3x2 + 3) . (x - 2)

Por lo que si a es una raíz de P(x), entonces P(x) se puede escribir como P(x)=Q(x) . (x-a)

Ejemplo: P(x)= x3 - 27

¿ Y una raíz?--- 3

Entonces se puede escribir:

P(x) = Q (x) . (x - 3) Que ya veremos cómo calcularlo.

Y esto ha sido la clase del viernes 14 de enero.

Paula Izco Oset 4ºA

Condiciones de las entradas mínimas:

Un resumen de la clase del día que corresponda, cuyo título incluya la fecha (y un título para la clase).